
Abbiamo già parlato del comportamento delle strutture tessili in caso di grandine in un articolo dedicato che potete rileggere qui ma data l’importanza del tema abbiamo voluto approfondire la questione con test su pannelli in ETFE singolo layer.
Dinamica della caduta della grandine
Possiamo immaginare la precipitazione di un chicco di grandine come il moto di una sfera pesante in caduta libera nell’aria, con
velocità iniziale nulla.
Durante la precipitazione il chicco di grandine risulta pertanto sottoposto alle sole azioni della forza di gravità, che trascina il chicco di grandine al suolo, e della resistenza dell’aria, orientata nel senso opposto all’avanzamento, che contrasta la discesa del chicco di grandine stesso. Per semplicità di analisi possiamo trascurare i fenomeni di disturbo dovuti a raffiche di vento trasversali e a correnti d’aria ascensionali, in modo da poter considerare la caduta della grandine perfettamente verticale. Questa ipotesi, estrema e improbabile, è generalmente peggiorativa, nel senso che dovrebbe massimizzare l’azione della grandine sulla superficie d’impatto.
Per un piccolo periodo iniziale, fin tanto che la resistenza dell’aria è trascurabile, il moto di un chicco di grandine potrebbe venire descritto dalle equazioni del moto uniformemente accelerato. Invece, all’aumento della velocità di caduta del chicco di grandine corrisponde un incremento della forza resistente dell’aria, in modo proporzionale al quadrato della velocità di avanzamento. La velocità di caduta aumenta progressivamente fino a quando la forza resistente (che aumenta progressivamente all’aumento della velocità di caduta) non equilibra la forza di gravità m*g (ovvero il peso del chicco di grandine). Le velocità calcolate ipotizzano una forma sferica del chicco di grandine. A questo punto il chicco di grandine risulta come non più sottoposto ad alcuna forza esterna e continua la sua caduta con velocità uniforme; detta velocità è la massima velocità raggiungibile dal chicco di grandine nella sua caduta libera attraverso l’aria, ed è detta velocità limite.
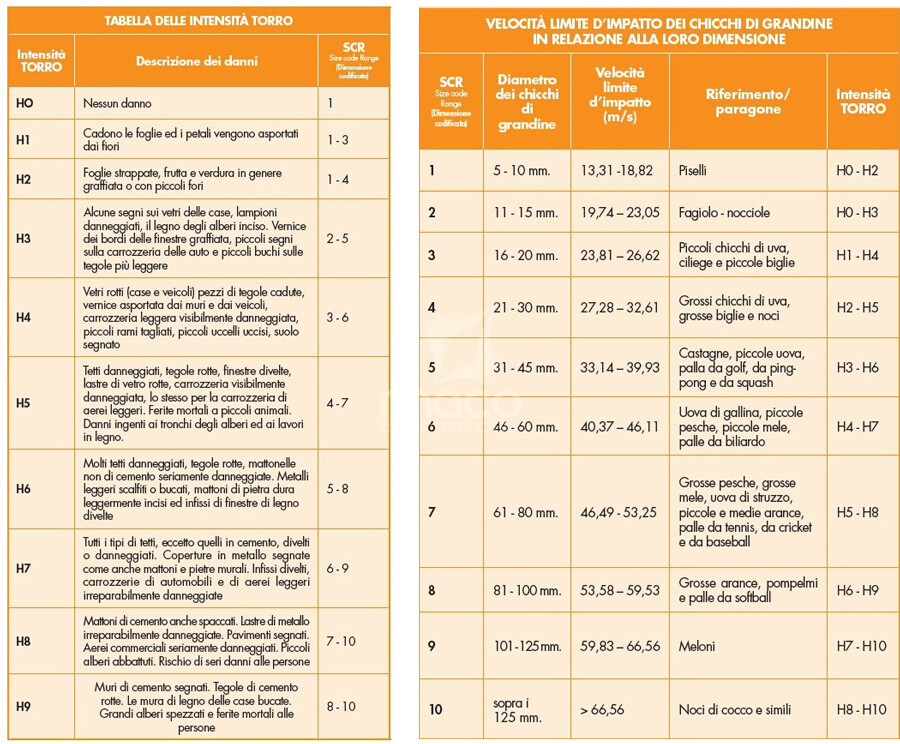
Al fine di avere un termine di paragone per i nostri futuri test, riportiamo nelle tabella seguente a sinistra, le descrizioni dei danni corrispondenti ai vari livelli di scala Torro. In quella di destra, invece, viene individuata la velocità limite di impatto dei chicchi di grandine in relazione alla loro dimensione.
Come si comporta l’ETFE, se colpito da una grandinata?
Al fine di toglierci ogni dubbio e dimostrare le proprietà meccaniche del film in ETFE, abbiamo deciso di realizzare una serie di test con l’obbiettivo di simulare cosa potrebbe accadere al film in caso di grandinata. Nella tabella seguente sono elencati gli oggetti che sono stati lanciati da circa 4.5 metri di altezza. Per paragonare gli urti tra di loro, abbiamo calcolato l’energia all’impatto (J) per ogni componente e abbiamo ricavato a cosa essa corrisponde in termini di grandine. Abbiamo anche evidenziato il livello corrispondente dell’evento meteorologico sulla Scala Torro che misura l’intensità degli uragani e dei suoi effetti (vento/grandine).
| massa (gr) | Velocità all’impatto (km/h) | Energia all’impatto (J) | Dimensione grandine | Massa (gr) | Velocità all’impatto (km/h) | Scala Torro | ||||
| sfera 1: | 40 | 34 | 1.76 | Equivalente | diam 20 mm | 3.8 | 95 | H3-H4 | ||
| dado 1: | 90 | 34 | 3.96 | Equivalente | diam 25 mm | 7.5 | 108 | H2-H5 | ||
| sfera 2: | 210 | 34 | 9.25 | Equivalente | diam 32 mm | 15.7 | 126 | H3-H6 | ||
| golfare: | 240 | 34 | 10.58 | Equivalente | diam 32 mm | 15.7 | 130 | H3-H6 | ||
| dado 2: | 260 | 34 | 11.46 | Equivalente | diam 32 mm | 15.7 | 137 | H3-H6 | ||
| pallina da tennis: | 47 | 150 | 39.5 | Equivalente | diam 40 mm | 30 | 150 | H3-H6 | ||
| grillo: | 960 | 34 | 42.32 | Equivalente | diam 45 mm | 43.7 | 158 | H3-H6 | ||
| cubo in acciaio: | 1050 | 34 | 46.29 | Equivalente | diam 45 mm | 43.7 | 165 | H3-H6 | ||
| palla da golf: | 46 | 200 | 69.57 | Equivalente | diam 50 mm | 60 | 172 | H4-H7 |
Risultati dei test
Dalle prove effettuate risulta evidente come l’ETFE riesca a resistere agli impatti più forti con deformazioni in campo elastico. Ciò accade per tutti gli oggetti senza spigoli acuminati quali le sfere, i dadi e i golfari. Nel caso di palline da golf, lanciate a 200 km/h, l’impatto genera una deformazione plastica nel film che però può essere rimossa attraverso l’uso di aria calda, come vedremo in una serie di test dedicati. Al contrario, oggetti appuntiti, sebbene abbiano una forza all’impatto inferiore, sono in grado di bucare l’ETFE. Si tratta per esempio dei casi del grillo o del cubetto in acciaio dal peso di circa 1kg. Risulta quindi evidente come l’ETFE sia in grado di resistere in modo eccellente alla grandine o alla caduta di oggetti anche molto grandi e lanciati a velocità alta a patto che non siano presenti elementi appuntiti che sarebbero potenzialmente in grado di attraversarne la superficie.
Ecco di seguito il video completo che che mostra i test su un pannello in ETFE da 300 micron.
